Cambridge IGCSE
TOPIC 4A: ELECTRICITY
All electric circuits transfer energy from a source of electrical energy, such as an electrical cell or mains supply, to the circuit components and then into the surroundings. This waste energy lost to the surroundings is typically heat energy. In fact, all resistances transfer electrical energy into heat. This is why a laptop may get warm when in use.
We often talk about electrical power and energy in similar terms. Power is just the energy transferred per second (see below) so when ever a device is turned on, it is transferring energy and therefore power.
If you have had the chance to carry out some experiments with cells and batteries at school, you will know that they are very safe to use. However the electrical sockets in homes, schools and offices are much more dangerous. The main reason for this is that the voltage is very high - typically 240 V in many countries. Japan and the USA use a lower 110 V to try to make it safer, but it is still very dangerous to humans and can deliver a potentially fatal electric shock.
Mains electricity is a.c., which stands for alternating current. The power station produces a current that constantly changes direction (a 50 Hz frequency in Europe). The power station that produces the electricity is effectively pushing and pulling electrons around the circuit. Note that an a.c. supply does not have a positive and negative terminal.
Cells, on the other hand, are d.c. - this stands for direct current, always flowing from positive to negative.
 |
DC supply symbol |
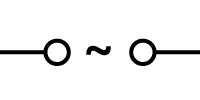 |
AC supply symbol |
Mains sockets are used around our homes for devices that need a bit more power, for example cookers, hairdryers and lighting. Power (P) is a physical measurement covered in a bit more detail in topic 3. It is basically a measure of the energy delivered per second, and has units of the watt (W).
For electrical devices, the power delivered depends on two factors - the current flowing through it, but also the voltage at which this current is 'forced through' the device. A higher voltage and a higher current will lead to a very high power output.
To calculate electrical power, we use this formula:
power = current x voltage
P = I x V
[watts] = [amps] x [volts]
Note that in this formula, the voltage is actually the p.d. across the component, in cases where there are several devices connected in series to the supply.
In addition to this formula, we can generate a formula to find the energy transferred.
The energy transferred can be found by multiplying the power by the time over which the appliance is on. (See topic 3).
This gives the following new formula:
energy = current x voltage x time
E = I x V x t
[joules] = [amps] x [volts] x [seconds]
Both these formulas are fairly straightforward, however watch out for power in kW (kilowatts), and time in minutes and hours. The formulas apply to both a.c. and d.c. voltages, and so can be used for questions with mains electricity and also with cells and batteries.
Many of the devices we use at home rely on the heating effect of a current. When a current passes through any resistor, the power produced is thermal power, and this heat can be used for cooking, drying hair and heating rooms.
The standard symbol for a heater or heating element looks like a resistor with vertical lines (see section 4.3, and question 2 below). All heaters are basically resistors!
Now we can take a look at typical questions on this section:
Example:
A 6V, 2A motor is left on for 30 seconds. Calculate:
(i) the power supplied to the motor
(ii) the energy transferred to the motor in this time
Answer:
(i) power = current x voltage so the power = 2 A x 6 V = 12 watts
(ii) energy = current x voltage x time = 2 A x 6 V x 30 = 360 joules.
Questions:
1. A 240 V toaster uses a current of 2A.
a) We know that P = I x V, so:
P = 2 x 240
P = 480 W
b) Firstly, remember to use 60 seconds, not 1 minute.
For this part of the question we can use E = I x V x t
E = 2 x 240 x
60
E = 28 800 J (or 28.8 kJ)
2. The diagram below shows two heating elements connected in series. The current flowing through the elements is 2.5 amps.

a) The p.d. across each element is 6 V, NOT 12 V.
Using P = I x V gives:
P =
2.5 x 6
P = 15 W each.
b) The total energy is given by E = I x V x t, and the total voltage is 12 V.
5 minutes = 300 seconds, so :
E = 2.5 x 12 x 300
E = 9000 J (9.0 kJ)
3. A 230 V, 2kW mains kettle is used to boil a litre of water. This requires 340 kJ of energy.
a) Mains is a.c., whereas a cell is a d.c. supply. (In addition, mains electricity is always much higher voltage than 9V, typically over 100 V worldwide).
b) We know P = I x V, so rearranging this gives:
| I = | P |
| V |
| I = | 2000 |
| 230 |
I = 8.70 amps
c) E = I x V x t can be rearranged to give:
| t = | E |
| I x V |
| t = | 340 000 | = | 340 000 |
| 8.7 x 230 | 2000 |
t = 170 seconds
(Note that we could have used the idea that E = P x t to solve part c, as the power is given in the question. If we use this method, then we get:
| t = | E | = | 340 000 |
| P | 2000 |
t = 170 seconds)
Extension
Fancy a challenge?
This question is hard, and is usually solved by learning a new formula at A level or IB physics level. However you can solve it without needing any other formulas apart from the ones covered so far in recent pages (sections 4.2a to 4.2e). Can you solve it?
Extension question:
A 60 mA current flows through a 1 kΩ resistor. What is the power lost as heat as current flows through the resistor?
When we use any appliance at home, the electricity comes at a cost - the supply company will measure how much energy has been used each month and then send a bill for payment. However, the unit of energy used in most places in the world in not the joule, as it is just too small.
To solve this, the idea that energy = power x time is used. The power of many appliances at home is high and is measured in kW (kilowatts). In addition, time periods are much longer than seconds, and typically devices are left on for hours. The new unit of energy called the kWh (kilowatt hour) is used. This is simply the power in kW multiplied by the time in hours.
The electricity supply company will charge a set fee for each 'unit' of energy, measured in kWh. As this is an international course, any type of money might be used as an example.

Figure 1: A home electric supply meter, measuring kWh
Kristoferb, C.C licence 3.0
Example:
A family go on holiday and accidentally leave a 2kW electric heater on for 7 days.
Calculate:
Answer:
(i) To find the energy used in kWh, simply multiply the power in kW by the time in hours.
7 days = 7 x 24 hrs = 168 hrs.
Therefore the family has used 2 kW x 168 hrs = 336 kWh.
(ii) If one kWh costs $0.19, then the total cost is:
0.19 x 336 = $63.84.
Question:
4. A 230 V, 1.2 kW electric oven is left on for 4 hours 30 minutes whilst cooking a large family meal.
a) To find the energy used, we just multiply the (power in kW) x (time in hours). Note that we do not need to use the voltage of the oven!
4 hrs 30 mins = 4.5 hrs
So E = 1.2 kW x 4.5 hrs = 5.4 kWh
b) If one unit costs 0.3 Euros, then the cost is:
0.3 x 5.4 =
1.62 Euros.
Now Try this quick 10 minute quiz on electrical power and energy: