Cambridge IGCSE
TOPIC 1A: FORCES and MOTION
When a force acts on something, many things can happen. However it is easier to summarise these into the following:
A force can either...
A force is basically a push or a pull on something. There are many different things that cause forces, but they are all measured in newtons (N) - the international unit for force.
Here are a few of the most common types of forces found in nature:

Figure 1. Lightning produced by electrostatic forces.
Friction is a general term for any force produced when an object is in contact with a solid, liquid or gas that pushes against the motion. If a liquid or gas is involved, we often call this force of friction the 'drag'. If it is an object like a plane moving through the air, we often call this type of friction air resistance.
Force is a vector as explained in section 1.1, and so can be drawn with an arrow. The length of the arrow can be used to show the size of the force, and obviously the direction of the arrow shows the direction of the force. The start of the arrow is placed on the object the force is acting on, as shown in figure 2 below.
If two or more forces are acting in the same direction, we can add them together to find the total.
However if they act in opposite directions, we need to subtract, as shown here by two forces acting on a ball:

Figure 2. Adding and subtracting forces
In both these diagrams, the ball will move to the right, because there is a 'total' force of 13 N or 3 N. This total is called the resultant force, and we say the forces are not balanced - they are unbalanced forces.
If both forces are equal in size but acting in opposite directions, the resultant force would be zero, and the forces would be balanced.
In many exam questions, one of the forces has a special description, like friction, air resistance, the force of gravity or weight (see section 1.5 for more about weight). However they are still forces and are simply drawn as arrows.
Questions:
1. A small van is travelling down a road. The forward force provided by the engine is 2 kN . The air resistance acting on the van is 600 N, and the friction between road and tyres is 300 N.
a) Calculate the resultant force acting on the van.
b) Describe the motion of the van at this point.
Imagine you are floating in space (in a space suit)! What would happen if you throw a ball in space? Where would it go?
In space there is no air, so no friction. As long as you are along way from stars and planets so there is no gravity, the ball would travel in a straight line, at the same speed, for many years. Any object must carry on at the same speed unless there is a force to change it's speed, such as friction to slow it down. This idea was first proposed by Isaac Newton, and is called Newton's 1st law. It is his most basic law, but says simply that:
Newton's 1st Law:
An object will continue to travel in a straight line at a constant speed, or remain at rest, unless acted on by a force.
This is a 'law' which means it is true for all objects, in all situations.
Take for example this tractor moving across a field:

Figure 3. A tractor driving through mud.
If the force from the engine is the same as the total force of friction from the mud (and air, wheels etc), then there is no resultant force acting. If there is no resultant force, Newton's 1st Law says that the tractor will stay at a constant speed and move in a straight line.
If the forward force increases, then there is now a resultant force forward and the tractor will change speed. In fact, any acceleration is the result of an unbalanced force, as described in the next section.
If the tractor is stationary with the engine switched off, there is no resultant force again and the tractor will remain at the same speed of zero! It will stay stationary.
Note: Remember that velocity is a vector quantity (has size and direction), so if the velocity is constant, the direction of motion must stay constant as well as the speed. This also means that if a force does change the velocity, it could change the speed, or it could also just change the direction of motion.
This is what is happening when the Moon orbits the Earth. The force of gravity from the Earth changes the direction the Moon is moving, to keep it going round in a circle. The speed of orbit does not change. (See the section on circular motion below).
Imagine your friend is a keen cyclist, and has entered a bike race. Does the bike they ride make a difference or is it just up to the cyclist to pedal hard?!
Does the mass of the bike make a difference?

Figure 4. bikes on a trail
Isaac Newton was considering how objects accelerate. He stated that - in this example - the bike acceleration at the start would depend on two things:
He realised there was a maths link between force, mass and acceleration, as stated here:
force= mass x acceleration
F = m x a
[newtons] = [kilograms] x [m/s2]
We can use kilograms for the mass, m/s2 for the acceleration, and the answer for the force will be in newtons (N).
This is a very famous formula and it makes it easy to find out how, for example, a bike might accelerate. Remember to convert any measurements to kg, N and m/s2 before putting the numbers into this formula.
Example:
An 800 kg boat accelerates away from a jetty with an acceleration of 0.3 m/s2. Calculate the force provided by the boat's engine.
Answer:
We know F = ma, and m= 800 g, a=0.3 m/s2.
Therefore F = 800 x 0.3 = 240 N.
Questions:
2. A mountain bike rider and bike together have a total mass of 80 kg. If the bike is to accelerate at 1.8 m/s2, what force needs to be applied?
3. A firework rocket of mass 200 g is set alight, and the force produced at the start is 5 N.
| a = | F |
| m |
| a = | 5 |
| 0.2 |
a = 25 m/s2
b) If a = 40 m/s2 and F = 5 N,
then F = ma gives:
| m = | F |
| a |
| m = | 5 |
| 40 |
Therefore m = 0.125 kg (or 125 g)
The experiment shown here is a standard way of showing how acceleration and force are linked, and frequently comes up in exams.
In this experiment, we are going to measure the acceleration of a toy car or trolley on a flat surface, typically a lab bench. We are going to use some weights (masses) to provide a force. We can time how quickly the car moves between 20 cm sections marked on the desk as shown here:
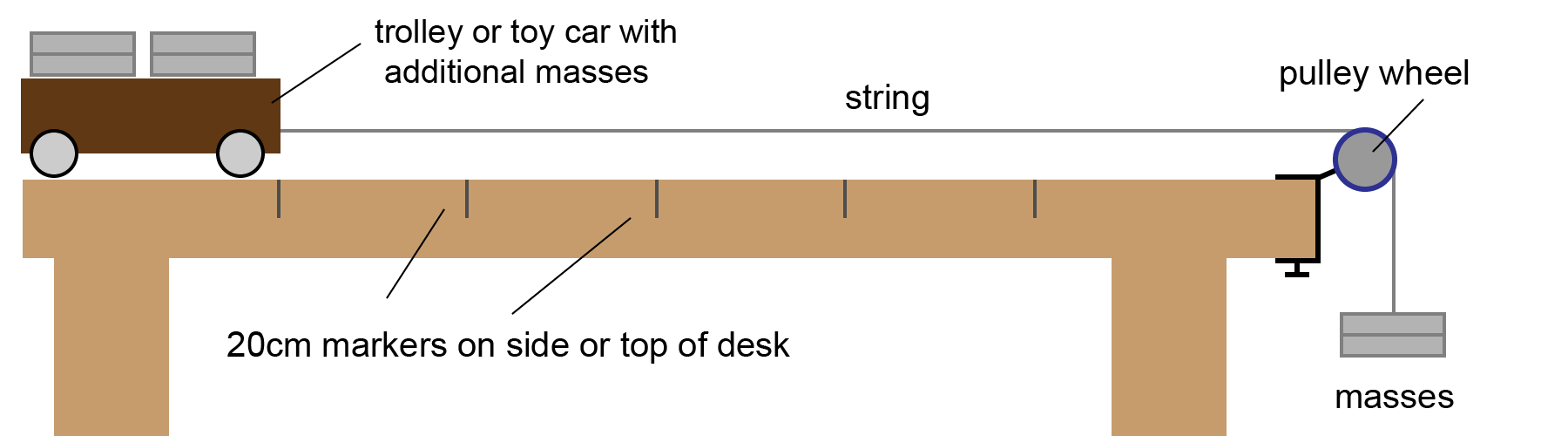
Figure 5: Investigating force, mass and acceleration
The speed of the car can be found for the first and last 20 cm sections. (Speed = distance ÷ time). We also need to know the time taken to move between these sections. We then have the change in speed, and the time taken. Then we can find the acceleration of the car.
This is a bit complicated involving several measurements, and is difficult to time if the trolley moves too quickly. It could be greatly simplified if we find the acceleration in one go with the use of light gates, as shown here. (This is a much better method if you have access to these devices, and a better method to describe in the exams).
Now we know the acceleration, we can see what effect the applied force or changing the mass has on this acceleration:
What will we find out?
The expected results are as per the formulas shown above, F= m x a.
Harder Question: 4. An elastic rope hangs down from the ceiling. It is stretched downwards, and attached to a 4 kg mass as shown here. The upwards pull from the rope when stretched is equal to 60 N. Calculate: a) The weight of the 4 kg mass. b) The resultant force acting on the mass. c) The initial acceleration of the mass. |
 |
a) W = mg, and so W = 4 x 9.8,
so W=39.2 N
b) Weight is a downwards pull of gravity and equals 39.2 N. if the upwards pull is 60 N, then the resultant = 60 -39.2,
so resultant force = 20.8 N upwards
c). We know F = ma, and that F is the resultant force, 20.8 N. This acts on the 4 kg mass. Rearranging the equation gives:
| a = | F |
| m |
| a = | 20.8 |
| 4 |
a = 5.2 m/s2.
To make an object change direction and move in a circle, you need to apply a force. This force is called a centripetal force. A simple example to illustrate this is the sport of hammer throwing:

Figure 6: The force needed for circular motion
Adapted from Ben Kasel CC BY-SA 4.0
The person throwing needs to pull hard on the large mass to keep it moving in a circle. As soon as it is released, it will fly out in a straight line. The force is directed towards the centre of the circle, and is always perpendicular to the direction of motion, and hence the velocity.
What factors would affect the pulling force needed to keep the mass rotating in a circle? There are only a few variables in this, including the radius of the circle, the mass of the object moving, and the velocity of the mass:
This should be common sense, but you will need to learn these effects to describe circular motion in a range of examples. For planets orbiting stars, the centripetal force is provided by gravity from the star. The animation below shows two planets of equal mass in orbit. Gravity increases in strength as you move towards the star. This means the nearest planet has a much stronger force acting on it. The stronger force is needed to move it in an orbit with a smaller radius, and it also makes it move at a higher velocity, taking less time to complete the orbit as shown here.
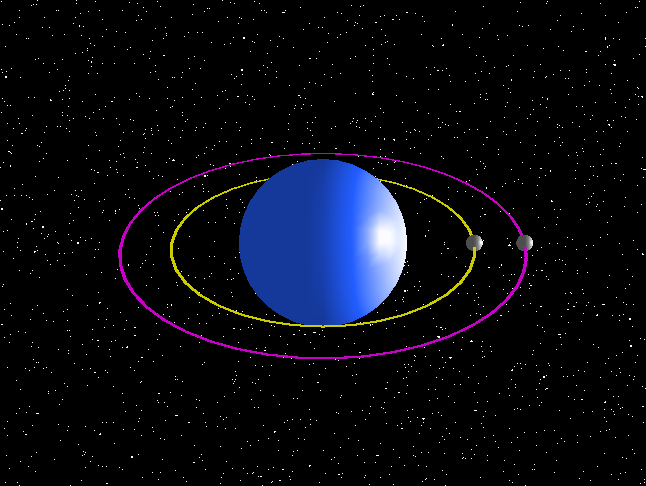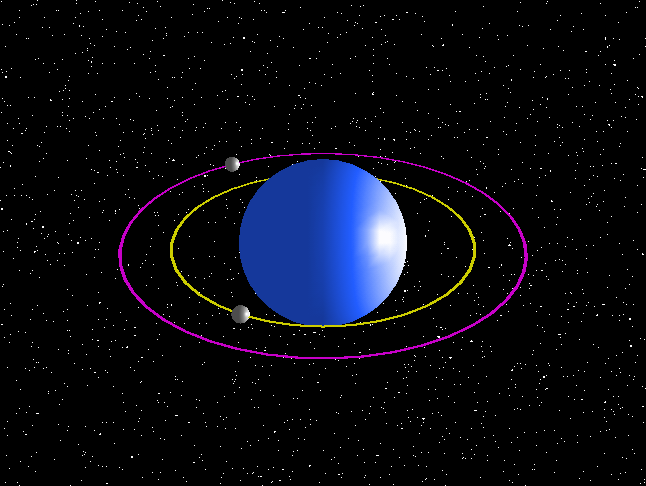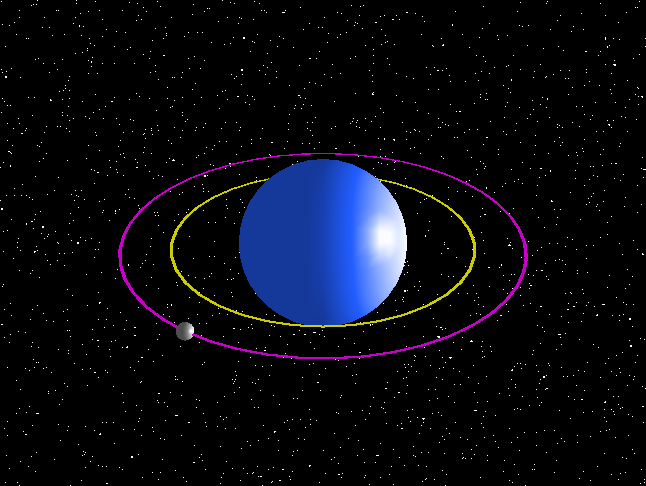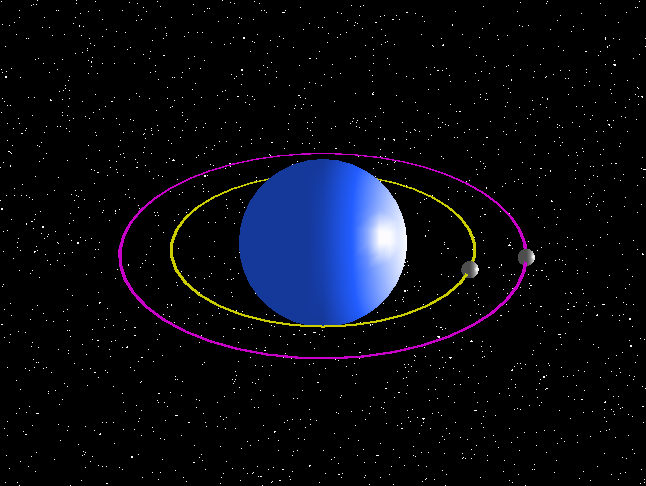
Figure 7: Simulation of 2 planets in orbit
GRC NASA
The maths formulas for circular motion are not required for IGCSE, and for orbits of planets it can get complicated! Just learn the three effects listed above for the IGCSE course.
Now test your understanding using these quick, 10 minute questions on Balancing Forces from Grade Gorilla: